Modelo de Wilson: la clave para la gestión óptima del stock

A fin de esquivar los problemas de inventario, el modelo de Wilson o EOQ (Economic Order Quantity - Cantidad económica de pedido, en su traducción al castellano) es un método matemático para calcular cada cuánto y en qué cantidad hay que realizar un pedido a un proveedor, garantizando así una adecuada gestión de stock.

Pese a que este modelo suele asociarse a la adquisición de materias primas y a la gestión óptima del stock, en realidad hay que tener en cuenta que la metodología Wilson puede aplicarse a cualquier tipo de mercancía.

Fórmula del Modelo de Wilson

Planteada originalmente en 1913 por el ingeniero norteamericano Ford Whitman Harris, no fue hasta 1934 cuando el consultor R.H. Wilson desarrolló la fórmula con éxito. Pero, ¿cómo se calcula?

A partir de la demanda de un producto, el coste de realizar un pedido y el gasto de almacenamiento podemos determinar el volumen óptimo de pedido. La fórmula matemática es la siguiente:

• Q= cantidad óptima de pedido
• D= demanda anual de la materia prima en cuestión
• K= coste de realizar cada pedido
• G= coste de almacenamiento de una unidad en el almacén en una cantidad de tiempo determinado

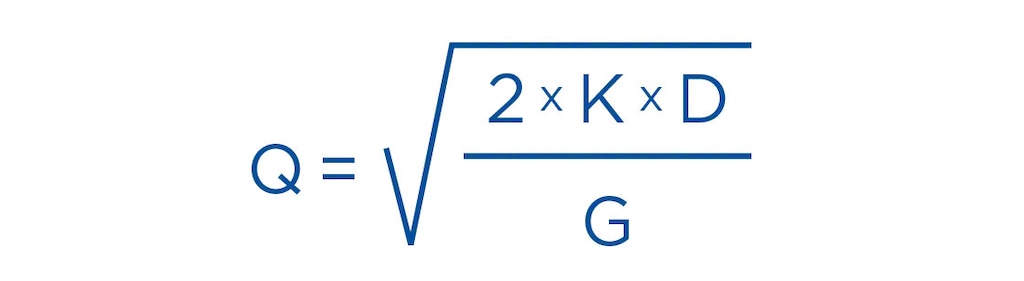
Aplicaciones y limitaciones

Este modelo matemático tiene como objetivo optimizar el volumen de compra de cualquier producto necesario, especificando cuándo hay que realizar un pedido a un proveedor y en qué cantidad.

Con este dato, podremos además determinar el punto de pedido (cuándo realizar cada pedido), teniendo en cuenta el lead time y el stock de seguridad. Sin embargo, el método de Wilson cuenta con ciertas restricciones. Esta solución matemática solo es aplicable a empresas en las que se cumplan las dos siguientes premisas:

• Que la compañía cuente con una demanda constante de materia prima durante todo el año
• Que el producto a adquirir mantenga un coste fijo atemporal, sin que haya grandes fluctuaciones en su precio a lo largo del año.

Si, por ejemplo, el coste de la materia prima varía según la temporalidad, esta fórmula matemática pasa a ser ineficaz, pues no tiene en cuenta esa variable.

En consecuencia, este método sólo es aconsejable para ciertas empresas en las que demanda y costes no sufran variaciones importantes a lo largo del año.

Ventajas del método

Para las empresas que cumplan ambas condiciones, este método matemático garantiza la optimización en la gestión del inventario. De hecho, esta solución presenta las siguientes ventajas:

• Minimizaremos los costes de adquisición y almacenamiento.
• Evitaremos los excesos de stock, pero asegurando que habrá el suficiente para atender la demanda en todo momento.
• Sabremos la cantidad correcta a adquirir en cada pedido.
• Evitaremos roturas de stock.

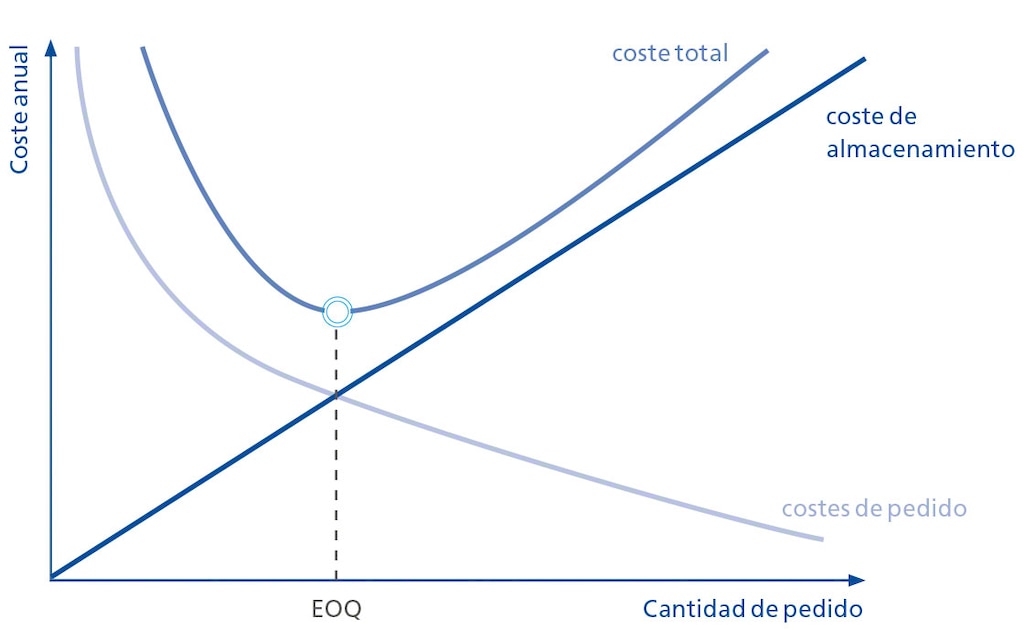
Ejercicio práctico del modelo de Wilson

La empresa imaginaria Orch Kork se dedica a la fabricación y distribución de corchos de botella para empresas vitícolas de la zona. Para cumplir con su producción anual de 10.000 unidades, la empresa adquiere a lo largo del año 1.000 kg de corteza de alcornoque.

Si cada pedido les cuesta 200€, en donde se incluyen también los gastos de transporte, y el coste de almacenamiento del producto no supera los 2.000€ anuales, ¿cuál es el volumen óptimo de pedido?

En este caso, Q (la cantidad óptima de pedido) se resolvería a partir de la raíz cuadrada de la siguiente fórmula (2*200*1000/2000), cuyo resultado es 14,14.

Orch Kork deberá realizar pedidos anuales de 14 kg con el fin de contar con una cantidad óptima de kilos de corteza de alcornoque para producir corcho, evitando así tanto el almacenamiento excesivo de la materia prima como la posible rotura de stock. Así pues, la compañía ha de efectuar 71 pedidos anuales de 14 kg para aprovisionarse de los 1.000 kg de corteza de alcornoque.

EOQ: minimizar costes de stock cuando no hay estacionalidad

En definitiva, gracias a aplicar el Modelo de Wilson en la gestión de su stock, la empresa lograría optimizar la adquisición de pedidos y así minimizar los costes totales de almacenamiento y compra. Eso sí, asumiendo que este modelo solo es aplicable cuando la demanda y los precios sean constantes a lo largo del año. Para situaciones más complejas, el modelo resulta inservible y en ese caso deberemos apoyarnos en un software de gestión de almacenes.